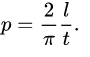[ #InternationalMathematicsDay Special]
So, here's collection of my favorite mathematical proofs. Hope y'all find those interesting. In case you wish to extend this, feel free to do so.
PS - Feel free to add citations/credits in case they are unknown.
So, here's collection of my favorite mathematical proofs. Hope y'all find those interesting. In case you wish to extend this, feel free to do so.

PS - Feel free to add citations/credits in case they are unknown.
(7) Proof that 22/7 > pi ( https://en.wikipedia.org/wiki/Proof_that_22/7_exceeds_%CF%80)
(8) A simple proof that π is irrational
Niven, Ivan. A simple proof that $\\pi$ is irrational. Bull. Amer. Math. Soc. 53 (1947), no. 6, 509. https://projecteuclid.org/euclid.bams/1183510788
Niven, Ivan. A simple proof that $\\pi$ is irrational. Bull. Amer. Math. Soc. 53 (1947), no. 6, 509. https://projecteuclid.org/euclid.bams/1183510788
(9) Fundamental theorem of algebra (Liouville):
From: https://www.ndsu.edu/pubweb/~novozhil/Teaching/452%20Data/12.pdf
Via Liouville's theorem:
From: https://www.ndsu.edu/pubweb/~novozhil/Teaching/452%20Data/12.pdf
Via Liouville's theorem:
(10) Proof of Bertrand's Postulate (Via: Wiki):
From: https://en.wikipedia.org/wiki/Proof_of_Bertrand%27s_postulate
From: https://en.wikipedia.org/wiki/Proof_of_Bertrand%27s_postulate
(11) Buffon's needle problem (via: Wiki):
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?
https://en.wikipedia.org/wiki/Buffon%27s_needle_problem
Answer:
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?
https://en.wikipedia.org/wiki/Buffon%27s_needle_problem
Answer:
(12) Proving Basel Problem using Fourier Series (unknown):
From: https://en.wikipedia.org/wiki/Basel_problem
From: https://en.wikipedia.org/wiki/Basel_problem
(13) Christoffel's Symbol using Euler Lagrangian Eqn: (Unknown)
From: Tong, David (Lectures of GR)
*- Note this is a special case of n-d flat manifold!
From: Tong, David (Lectures of GR)
*- Note this is a special case of n-d flat manifold!
Help extending the list! :-)

 Read on Twitter
Read on Twitter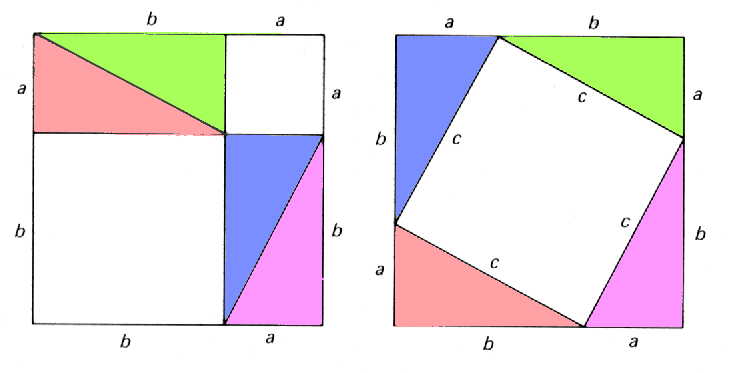
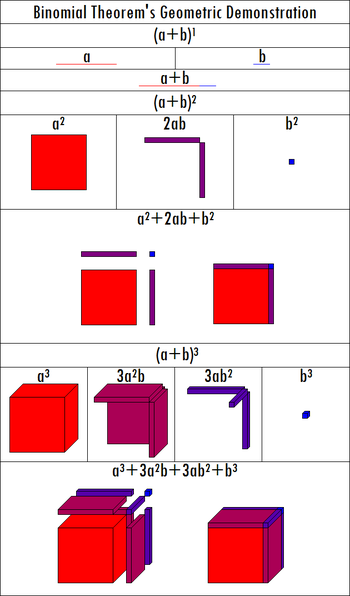

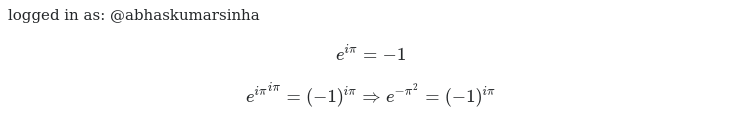
![(5) Proving Euler's Identity [1/2] (By Unknown): (5) Proving Euler's Identity [1/2] (By Unknown):](https://pbs.twimg.com/media/Ep2qSJqUYAEHrkH.png)
![(6) Proving Euler's Identity [2/2] : (6) Proving Euler's Identity [2/2] :](https://pbs.twimg.com/media/Ep2qZ6AVoAAWkCu.png)