Our results on Lattice surgery for quantum error correction have been published with @SpookyQuantifex and @QuantumTales (others not on twitter) https://www.nature.com/articles/s41586-020-03079-6
This is a collaboration with @iqoqivienna via @FWF_at and @ETH_physics via @AQTION_eu @QuantumFlagship . 1/n
This is a collaboration with @iqoqivienna via @FWF_at and @ETH_physics via @AQTION_eu @QuantumFlagship . 1/n
Lattice surgery is a method that can enable multi-qubit operations in a fault tolerant quantum computer. See paper
https://iopscience.iop.org/article/10.1088/1367-2630/14/12/123011 with @rdviii. Lattice surgery allows one to perform operations between logical qubits by manipulating the boundaries of the two codes. 2/n
https://iopscience.iop.org/article/10.1088/1367-2630/14/12/123011 with @rdviii. Lattice surgery allows one to perform operations between logical qubits by manipulating the boundaries of the two codes. 2/n
This is efficient, as the standard method of performing operations between two logical qubits requires transversal operations on the entire surface. Lattice surgery is even more powerful, as it allows to switch between different codes. We entangled two logical qubits. 3/n
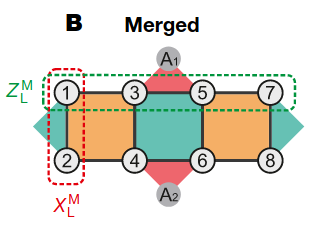
In the experiment, we encoded two logical qubits in 2x4 physical qubits. The orange and green surfaces indicate the many-body stabilizers that define the code. This is not a full error correction code yet, but it represents the smallest instance of a surface code: 4/n
We merge these two logical qubits into a single qubit by preparing the stabilizers on the boundary in a well defined state. For this, two additional auxiliary qubits are required. 5/n
We can split the logical qubit in two qubits again using an auxiliary qubit. The logical information in the two qubits is then entangled. 6/n
The entanglement process can be illustrated by the logical information in the system at each point during this procedure. At the beginning the two logical qubits are in an Eigentstate of the logical Z operator: 7/n
After the merge, the individual logical Eigenvalues are not defined anymore. The information is in the joint logical operations ZZ,XX,YY. But there is only a single logical qubit left. 8/n
After the split, the joint Eigenvalues are preserved. We have now two logical qubits, where all single-qubit Eigenvalues are zero, but the Eigenvalues of the two-qubit Pauli operators are ideally 1. This are the properties of an entangled Bell state of the two logical qubits 9/n
This entanglement generation is one of the hallmark features of Lattice surgery. This method can be used to perform logical operations by teleported gates (also in the paper) 10/n
But of course there is a lot to do. 1.) It is an error detection code where not all single qubit errors are correctable. This is not sufficient to run long algorithms, although we see that errors are reduced when we discard all experimental runs where we detect an error. 11/n
2.) The gates we are using are not fault tolerant. That means that not all errors coming from our operations can be detected by the code. We are currently developing a gate set that will allow fault tolerant circuit construction. 12/n
If you made it this far, here is a happy dog in fresh austrian snow

 Read on Twitter
Read on Twitter